MAXIMA AND MINIMA OF FUNCTIONS

TO FIND THE MAXIMA AND MINIMA OF FUNCTIONS FOLLOWING STEPS ARE FOLLOW:

• Let the given function is Y=0.
• Now differentiate the function w.r.t. to X.
• Differentiate of Y w.r.t. X is slope of curve.
• Now minimum and maximum, put slope of curve is zero.
• From above condition we get value of X.
• Now double differentiate the Y.
• Now put the value of X in Double differentiate.
• If double differentiate is less than zero then maxima will be occur at that point.
• If double differentiate is greater than zero then minima will be occur at that point.
• If double differentiate is  zero then that point is called saddle point.

          

For example:

Let f(x)= y = x³ − 6x² + 12x − 5

now differentiate w.r.t. to X.
that is
y = 3x² − 12x + 12 
For minima and maxima put Y=0
that is 3x² − 12x + 12=0

we get X=2 only

Now double differentiate of f(x)
y'' = 6x − 12
 put X=2 in the double derivative we get
y''=6*2-12=0
hence the test is fail and at X=2, the curve has neither has maxima and minima. This point is called saddle point.

EXAMPLE:
 Find the maxima and minima for:
y = 5x³ + 2x² − 3x

Now first differentiate and find the slope of curve.
i.e.

y’=15x²+4x-3
put slope is equal to zero i.e. 15x²+4x-3=0
we get

x = −3/5 and x = +1/3

Now double differentiate the function we get

y″=30x+4

Now at x = −3/5 value of y″=30(-3/5)+4=(-14)

and

at x = +1/3

y″=30(1/3)+4=14

Hence y″<0 at x = −3/5 and y″>0

from this we can conclude that the function has maxima at  x = −3/5 minima at x = +1/3

THE GRAPH OF FUNCTION IS SHOWN BELOW:

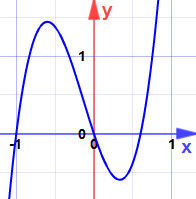
Determine the maxima and minima of the function y=x³-x²-x+1.

First find the slope of the function

y′=3x²-2x-1

slope is zero when 3x²-2x-1=0

when

3x²-2x-1=0

3x²-3x+x-1=0

3x(x-1)+1(x-1)=0

(3x+1)(x-1)=0

from this x=(-1/3) and x=1

find double differentiation i.e. y″

y″=6x-2

y″(-1/3)=6×(-1/3)-2

y″(-1/3)=-4

and x=1

y″(1)=6×1-2=4

y″(1)=4

y″(1)>0 hence function has minima at x=1.

and

y″(-1/3)<0 hence function has maxima at x=-1/3

Minimum value

y(1)=1³-1²-1+1=0

and

Maximum value

y(-1/3)=(-1/3)³-(-1/3)²-(-1/3)+1=1.185

y(-1/3)=1.185

LINEAR EQUATIONS WITH TWO VARIABLES

THE EQUATIONS WITH TWO VARIBLES x AND y CALLED LINEAR EQUATIONS WITH TWO VARIABLES.

Solve the following system of linear equations:

{y=2x+4y=3x+2

Now from equation 1 put value of y in equation 2
we get
        y=3x+2
2x+4=3x+2
      4-2=3x-2x
         2=x
Hence x=2
Now putting value of x=2 in equation 1 we get,
y=2x+4
y=2*2+4
y=8

SOLUTION OF THESE TWO EQUATION  x=2 and y=8

 solutions of these two equations of straight line, solution of these two equations are inter section of line.

QUADRATIC EQUATIONS

QUADRATIC EQUATIONS 

THE EQUATION IN THE FORM OF  IS CALLED QUADRATIC EQUATION. WHERE a, b AND c ARE CONSTANT.
SOLUTION OF QUADRATIC EQUATION IS GIVEN BY.


Meaning of the root of the equations in geometric term:

The roots of the quadratic equations represent, since the quadratic equation represent the equation of parabola. hence the root of  the quadratic equations where the parabola cut the x-axis.

in the given below the curve of parabola cut the x-axis at x= -1 and 2 hence the -1 and 2 are the roots of the equations




Thus according to the value of the (b²-4ac) there can be three conditions are possible:
1. If (b²-4ac)>0
then roots are real and distinct
and the parabola cut the axis at two points

2. If (b²-4ac)=0
then the roots are real and equal 
hence the parabola touch the axis




3. If (b²-4ac)<0
then the roots are imaginary
hence the parabola not cut or touch the axis.

For Example:

Solve x2 + 3x – 4 = 0

Factor method

x²+3x-4=0

using facorization method

x²+4x-x-4=0

x(x+4)-1(x+4)=0

(x-1)(x+4)=0

x=1 and x=-4

What is the root of x2+6x+5=0?
x²+5x+6=0

using factor method

x²+3x+2x+6=0

now taking the x common from first two term and 2 from last two term

x(x+3)+2(x+3)=0

taking (x+3) common

(x+3)(x+2)=0

x=-2 and x=-3

hence the root of quadratic equation are -2 and -3

What is the value of x in the equation  x3−6x2+11x−6=0

Since x=1 is satisfying the equation x³-6x²+11x-6 hence x=1 is the root of the equations

i.e.

x³-6x²+11x-6=1³-6×1²+11×1-6=0

hence divide equation by (x-1)

i.e.

x-1⟦x³-6x²+11x-6⟧x²-5x+6

       x³-x²

       ——

          -5x²+11x-6

          -5x²-5x

           ————

                 6x-6

                 6x-6

              —————

                    0

i.e.

x³-6x²+11x-6=(x-1)(x²-5x+6)

                      =(x-1)(x²-3x-2x-6)

                     0=(x-1)(x-2)(x-3)

hence 

x=1, x=2 and x=3

If one root is equal to the square of the other root of the equation x^2 + x - k = 0, what is the value of k?
Given equation

x²+x-k=0

Let one of the root is α then other root will be α²

Now, 

sum of root(α+α²)=-1

product of roots α³=-k

then α=-k

and

k+k²=-1

k²+k+1=0

k=-1±√(1-4)/2

k=-1±√3i/2

hence the value of k are -1+√3i/2 and -1-√3i/2

Note: Value of k are imaginary.

If 1-i is a root of the equation x2+ax+b=0, then what is the value of a and b?

If 1-i is one root then other root will be 1+i because roots are imaginary

Now

sum of roots=1-i+1+i=-a

i.e. a=-2

and

product of roots=(1-i)(1+i)=(1-i²)

=1+1=2=b

b=2

1. Solve for x

x²=2x+1

x²-2x-1=0

x²-x-x-1=0

x(x-1)-1(x-1)

(x-1)(x-1)=0

x=1,1

2. Solve for x

2x²+7x+6=0

2x²+4x+3x+6=0

2x(x+2)+3(x+2)=0

x=-2 and x=-3/2

3. If sin C and cos C are two roots of the quadratic equation 2x^2-px+1=0 where 0<c<π/2, then how many possible values can p have?
2x²-px+1=0

roots are sinx and cosx

sum of roots sinx+cosx=p/2

and product sinx cosx=1/2

sinx+cosx=p/2

squaring on both sides

sin²x+cos²x+2sinx cosx=p²/4

1+2sinx cosx=p²/4

1+2×(1/2)=p²/4

2=p²/4 or p²=8

p=2√2 and p=-2√2

If the quadratic equation ax²-bx+3=0 and x²-4x+1=0 have a common root, then what is the area of rectangle having sides a and b?  

ax²-bx+3=0 and x²-4x+1=0

let the root are x and y

then x+y=b/a and x+y=4

and  x+y=3/a and xy=1

now solve for x and y

then a and b\

now area of rectangle is a×b

For Example:

DIFFERENTIAL EQUATIONS

How to solve 
$x{\displaystyle }$dydx−y=x3+3x2−2x

How do I solve dy/dx +ytanx =sin2x, where y(0) =1?

What is the value of the derivative of log (base a) x?

y=log_ax

y=logx/loga

dy/dx=(1/x)/loga

dy/dx=log_ae/x