QUADRATIC EQUATIONS

QUADRATIC EQUATIONS 

THE EQUATION IN THE FORM OF  IS CALLED QUADRATIC EQUATION. WHERE a, b AND c ARE CONSTANT.
SOLUTION OF QUADRATIC EQUATION IS GIVEN BY.


Meaning of the root of the equations in geometric term:

The roots of the quadratic equations represent, since the quadratic equation represent the equation of parabola. hence the root of  the quadratic equations where the parabola cut the x-axis.

in the given below the curve of parabola cut the x-axis at x= -1 and 2 hence the -1 and 2 are the roots of the equations




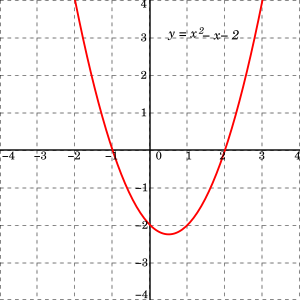
Thus according to the value of the (b²-4ac) there can be three conditions are possible:
1. If (b²-4ac)>0
then roots are real and distinct
and the parabola cut the axis at two points

2. If (b²-4ac)=0
then the roots are real and equal 
hence the parabola touch the axis




3. If (b²-4ac)<0
then the roots are imaginary
hence the parabola not cut or touch the axis.

For Example:

Solve x2 + 3x – 4 = 0

Factor method

x²+3x-4=0

using facorization method

x²+4x-x-4=0

x(x+4)-1(x+4)=0

(x-1)(x+4)=0

x=1 and x=-4

What is the root of x2+6x+5=0?
x²+5x+6=0

using factor method

x²+3x+2x+6=0

now taking the x common from first two term and 2 from last two term

x(x+3)+2(x+3)=0

taking (x+3) common

(x+3)(x+2)=0

x=-2 and x=-3

hence the root of quadratic equation are -2 and -3

What is the value of x in the equation  x3−6x2+11x−6=0

Since x=1 is satisfying the equation x³-6x²+11x-6 hence x=1 is the root of the equations

i.e.

x³-6x²+11x-6=1³-6×1²+11×1-6=0

hence divide equation by (x-1)

i.e.

x-1⟦x³-6x²+11x-6⟧x²-5x+6

       x³-x²

       ——

          -5x²+11x-6

          -5x²-5x

           ————

                 6x-6

                 6x-6

              —————

                    0

i.e.

x³-6x²+11x-6=(x-1)(x²-5x+6)

                      =(x-1)(x²-3x-2x-6)

                     0=(x-1)(x-2)(x-3)

hence 

x=1, x=2 and x=3

If one root is equal to the square of the other root of the equation x^2 + x - k = 0, what is the value of k?
Given equation

x²+x-k=0

Let one of the root is α then other root will be α²

Now, 

sum of root(α+α²)=-1

product of roots α³=-k

then α=-k

and

k+k²=-1

k²+k+1=0

k=-1±√(1-4)/2

k=-1±√3i/2

hence the value of k are -1+√3i/2 and -1-√3i/2

Note: Value of k are imaginary.

If 1-i is a root of the equation x2+ax+b=0, then what is the value of a and b?

If 1-i is one root then other root will be 1+i because roots are imaginary

Now

sum of roots=1-i+1+i=-a

i.e. a=-2

and

product of roots=(1-i)(1+i)=(1-i²)

=1+1=2=b

b=2

1. Solve for x

x²=2x+1

x²-2x-1=0

x²-x-x-1=0

x(x-1)-1(x-1)

(x-1)(x-1)=0

x=1,1

2. Solve for x

2x²+7x+6=0

2x²+4x+3x+6=0

2x(x+2)+3(x+2)=0

x=-2 and x=-3/2

3. If sin C and cos C are two roots of the quadratic equation 2x^2-px+1=0 where 0<c<π/2, then how many possible values can p have?
2x²-px+1=0

roots are sinx and cosx

sum of roots sinx+cosx=p/2

and product sinx cosx=1/2

sinx+cosx=p/2

squaring on both sides

sin²x+cos²x+2sinx cosx=p²/4

1+2sinx cosx=p²/4

1+2×(1/2)=p²/4

2=p²/4 or p²=8

p=2√2 and p=-2√2

If the quadratic equation ax²-bx+3=0 and x²-4x+1=0 have a common root, then what is the area of rectangle having sides a and b?  

ax²-bx+3=0 and x²-4x+1=0

let the root are x and y

then x+y=b/a and x+y=4

and  x+y=3/a and xy=1

now solve for x and y

then a and b\

now area of rectangle is a×b

For Example: