CONTINUITY

CONTINUITY 

Continuity means unbroken curve within the given limit.

In other words if we can draw the given curve without lifting the pen from the paper within the given limits then the given function is called the continuous function otherwise discontinuous.

 for example:

Above function is continuous because the curve is continuous and can be drawn without lifting the pen from the paper within the domain.

Another Example:

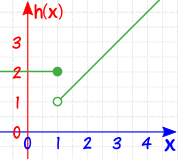
The above function h(x) is discontinuous at X=1, because at X=1, the curve is unbroken.

or

The function h(x) is discontinuous because we have to lift the pen from the paper to draw the curve at X=1.

How to find the continuity of the function.

for function to be continuous the left hand side and right hand side of the limit at the point must be defined and should equal and equal to the value of the function at the given point.

Let the given point is c. 

then for continuous function value at LHS= value at RHS = value the point c

For example:

Example: f(x) = (x²-1)/(x-1) for all Real Numbers

Now calculate the LHS limit and RHS limit

LHS limit that is at point just less than 1 that is (1-h) where h➡️0.

LHS limit

f(x)= ((1-h)₂-1)/(1-h-1)

on solving this limit h➡️0.

we get

f(x)=2

RHS limit

RHS limit that is at point just greater than 1 that is (1+h) where h➡️0.

f(x)= ((1+h)₂-1)/(1+h-1)

on solving this limit h➡️0.

we get

f(x)=2

and limit at X=2

f(x)=(x-1)(x+1)/(x-1)

f(x)=(X+1)

we get

f(x)=2

hence

value at LHS= value at RHS = value the point X=1
Hence the given function is continuous at X=1

:

Another example

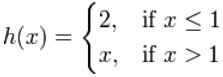
Now calculate the LHS limit and RHS limit

LHS limit that is at point just less than 1 that is (1-h) where h➡️0.

for LHS limit 
that is for X less than 1, value of function is 2
LHS limit 

h(x)=2

And RHS limit

that is for X greater than 1, value of function is
RHS limit 

h(x)=(1+h)

where h➡️0.

we get 

h(x)=1

and the value of function at X=1 is 2

hence LHS limit not equal to RHS limit

The given function is discontinuous at X=1