POINTS
Point is represented by dot. A point has position but not size.
Example:
A point on the line.
A point in the space.
here point P,Q and R are on the line
and
Point X,Y and Z in the space.
In two dimensional point can be any of the four quadrant.
i.e.
- First quadrant: In which both x and y co-ordinate are positive. It is represented by (+x,+y)
- Second quadrant:In which x is negative and y co-ordinate is positive. It is represented by (-x,+y)
- Third quadrant: In which both x and y co-ordinate are nagetive. It is represented by (-x,-y)
- Fourth quadrant:In which x is positive and y co-ordinate is nagetive. It is represented by (+x,-y)

DISTANCE BETWEEN TWO POINTS:
If the two points A and B of coordinate (x1,y1) and (x2,y2) are given then the distance between AB is given by the following formula.
For example:
Let the two points are (3,2) and (7,8)

Distance formula=
AB=√(7-3)²+(8-2)²
Mid point formula
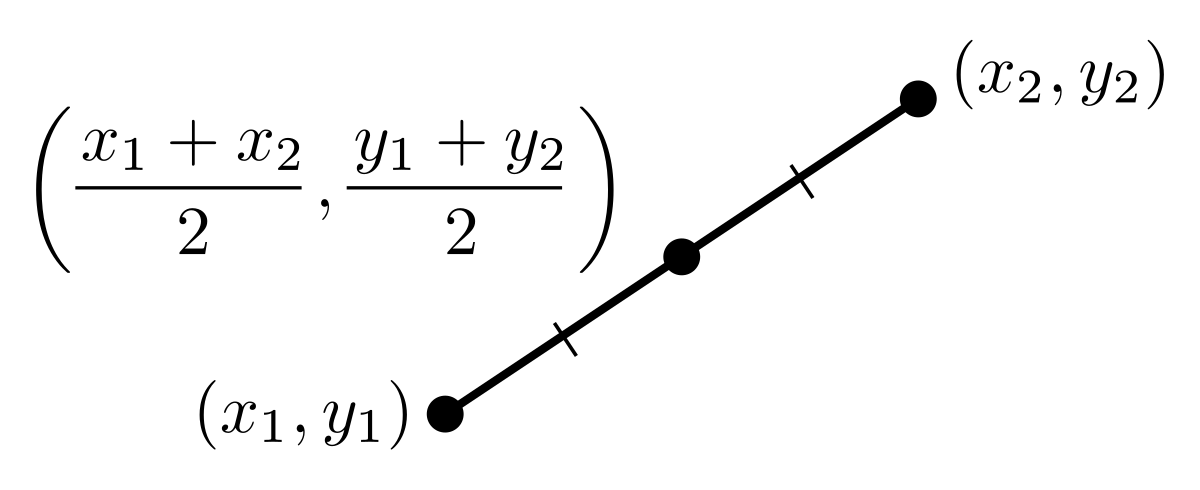
Find the value of K if the points A(3k, k) and B(3k+1, k-3) are equidistant from the origin.
2. Find the distance between following points
AB=√4²+6²
AB=√16+36
AB=√52
Mid point formula
If the two points A and B of coordinate (x1,y1) and (x2,y2) are given then the mid point of AB is given by the following formula.


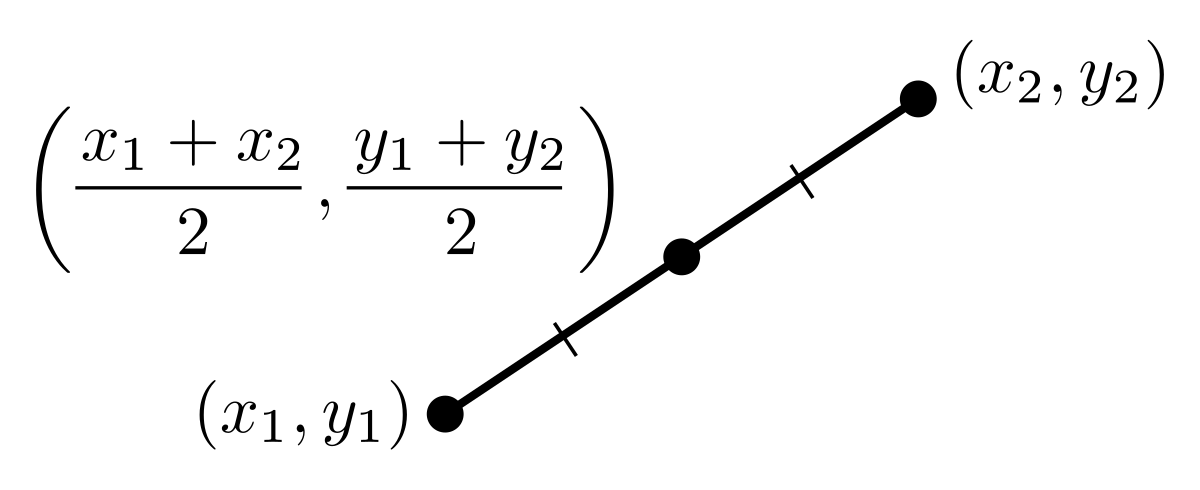
Find the value of K if the points A(3k, k) and B(3k+1, k-3) are equidistant from the origin.
Distance formula= √(x-x1)²+(y-y1)²
where (x,y) are given point and (x1,y1) are origin.
then
√((3k)²+k²)=√((3k+1)²+(k-3)²
sovle for k
(3k)²+k²)=(3k+1)²+(k-3)²
9k²+k²=9k²+1+6k+k²+9-6k
simplfy
0=10
conclusion: for all value of k, points A(3k, k) and B(3k+1, k-3) are equidistant from the origin.
Work for you:
1. Find the quadrant in which following points lie:- (5,2)
- (-2,-2)
- (3,-3)
- (-2,1)
2. Find the distance between following points
- (5,2) and (2,5)
- (-3,-3) and (-2,-2)
- (1,2) and (-2,1)
- (5,-2) and (-2,5)
- (3,3) and (-2,-2)
- (2,-1) and (-2,1)

No comments:
Post a Comment